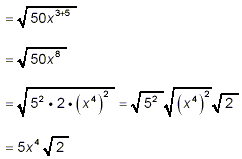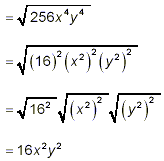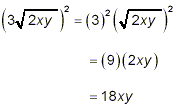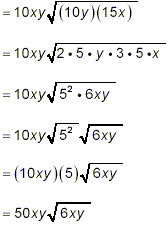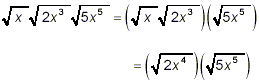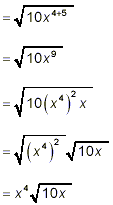Multiplying and Dividing With Square Roots

We have already looked in some detail at multiplication and division with numerical square roots. The rules for multiplication and division with algebraic square roots are exactly the same as those for numerical square roots – in fact, we stated those rules there in an algebraic form:

property 1

and

property 2

where ‘a’ and ‘b’ stand for any valid mathematical expression.

When expressions involving square roots are to be multiplied or divided, just use the above rules to combine square roots as necessary. Then simplify the resulting expression as much as possible using methods of simplification already described and illustrated extensively in the preceding documents in this series.

The examples following below illustrate this general strategy, but also provide some examples for your own practice.

Example 1:

Simplify

solution:

Using property (1) above,

as the final answer.

Example 2:

Simplify

solution:

Using property (1) above, we get

Example 3:

Simplify

solution:

You could regard this problem as a product

and use the procedures illustrated in the previous examples. However, an even faster way to get the answer is to distribute the power 2 over all factors in the brackets:

as the final answer. Here we have used the basic fact that´.

Example 4:

Simplify

solution:

as the final simplified answer.

Example 5:

Simplify

solution:

This is a product of three square root factors, and so does not fit property (1) at the beginning of this document precisely. However, we can apply property (1) in a stepwise fashion

So

which now does match property (1). Continuing

as the final simplified result.

The obvious implication of this stepwise application of property (1) is that property (1) can be extended to products of any number of square root factors.