Adding and Subtracting Fractions
Now we can apply these concepts to working with fractions.
To add or subtract fractions with the same denominator (bottom), simply add or subtract
the numerators (top).
Example:
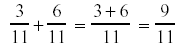
Example:
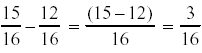
To add or subtract fractions with different denominators (bottom), we must change the
fractions so the denominators match. You can use any matching denominator, but finding
the denominator with the least common multiple gives you the simplest arithmetic.
Example:
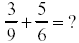
Step 1:
First we must change the fractions so they have the same denominator.
We start by finding the least common multiple of the numbers 6 and 9:
Multiples of 9 are 9, 18, 27, 36 ....
Multiples of 6 are 6, 12, 18, 24, 30 ....
The least common multiple is therefore 18.
Step 2:
Change the fractions by multiplying the numerator and denominator by the
factor which will make the denominator l8:
For the first fraction
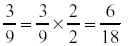
For the second fraction
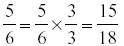
Step 3:
Now we can add the two fractions:
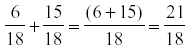
Step 4:
We always reduce our fractions, and notice both 21 and 18 are divisible by
3. (The greatest common factor is three.)
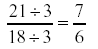
The answer to the above example, 7/6, is called an improper fraction, because the
numerator is larger then the denominator. We convert this into a mixed number, which is
a number that contains a whole number. Do this by dividing 7 by 6 and showing the
remainder as a fraction.
Example:
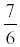 is the same as 7 divided by 6. is the same as 7 divided by 6.
6 goes into 7 once with remainder 1.
The mixed number is
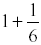 , which is written
as , which is written
as
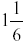 |