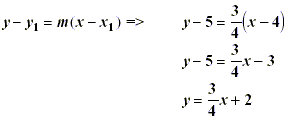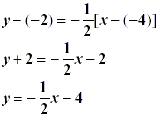|
Writing Linear EquationsWriting linear equations for a graph.If the graph is nonvertical: • Determine the y -intercept ( b) • Determine the slope using rise over run (m ) • Write a linear equation using y = mx + b and replacing m and b with the values you found If the graph is vertical: • Determine the x -intercept ( a ) • Write a linear equation using x = a and replacing a with the value you found
Writing a linear equation for a given point and slope.Example Write a linear equation with a slope of 2 and containing the point (-3, 5). Use the point-slope form for a linear equation: y - y 1 = m ( x - x 1 ) Substitute the values into the equation as follows: y - 5 = 2( x - (-3)) y - 5 = 2 x + 6 y = 2 x + 11
Writing a linear equation with 2 given points:Example Given (0, 2) and (4, 5), write a linear equation
First determine the slope of the line:
Then use the point-slope form to write the equation. Use either point.
Writing a Linear Equation for a graph described by a 2nd equation.• In all cases, find the slope and a point on the line to solve. Example A line passes through the point (3, 2) and has the same slope as the the line for y = -2x + 5. m = -2 for both lines so... y - 2 = -2( x - 3) y - 2 = -2x + 6 y = -2 x + 8 Example A line passes through the point (-4, -2) and is parallel to the line 2 x + 4 y = 4. Find the slope of the line 2 x + 4 y = 4 4 y = -2 x + 4
therefore
Example A line passes through the point (2, 5) and is perpendicular to the line - x + 3 y = -2. Find the slope of the line - x + 3 y = -2. 3 y = x - 2
If the slope of - x + 3 y = -2 is y - 5 = -3( x - 2) y - 5 = -3 x + 6 y = -3 x + 11 |
|