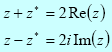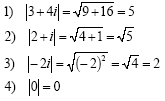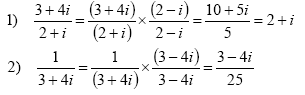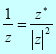Complex Numbers

A complex number is an expression of the form x + iy where x and y are real numbers.

Either x or y may be equal to zero: real numbers and imaginary numbers are special cases of complex numbers.

Given a complex number z = x + iy the real number x is known as the real part of z and the real number y is known as the imaginary part of z.

The notation Re is used for real part and Im is used for imaginary part.

Note that the imaginary part of z is a real number y (NOT iy).

Adding and Subtracting Complex Numbers

To add or subtract complex numbers, we add or subtract their real and imaginary parts separately:

Examples:

1) (2 + 3i) + (4 + i) = 6 + 4i

2) (3 - 5i) - 7i = 3 - 12i

3) (5 - 4i) + (3 + 2i) - (8 + i) = -3i

4) 12 - 4i + (3 + 4i) = 15

Multiplying complex numbers

To multiply complex numbers, we use the usual rules and the identity i² = -1:

Examples:

The complex conjugate

Given a complex number z = x + iy, the complex conjugate is given by z^* = x - iy (pronounced “z star”):

To find the complex conjugate of any expression, replace i by –i.

Examples:

1) (3 + 4i)^* = 3 - 4i

2) (5 - 2i)^* = 5 + 2i

3) (6i)^* = -6i

4) [(2 + 4i)^*]^* = [2 - 4i]^* = 2 + 4i

The last expression demonstrates that

A complex number and its complex conjugate have the property that:

Examples:

1) (3 + 4i) + (3 + 4i)^* = 3 + 4i + 3 - 4i = 6

2) (3 + 4i) - (3 + 4i)^* = 3 + 4i - 3 + 4i = 8i

3) 5i + (5i)^* = 5i - 5i = 0

4) 5i - (5i)^* = 10i

Complex conjugate of a product

The modulus of a complex number

A complex number z = x + iy multiplied by its complex conjugate is a real number:

The modulus of a complex number z = x + iy is written | z | and is equal to the positive square root of the sum of the squares of its real and imaginary parts:

Examples:

The modulus is a real number

The quotient of complex numbers

In order to simplify an expression with a complex number in the denominator, we multiply both the numerator and denominator by the complex conjugate:

In this way, we get a real number in the denominator (the modulus squared of a + bi).

Examples:

In general: